[논문리뷰] NFnet-High Performance Large Scale Image Recognition Without Normalization
안녕하세요. 오늘은 정말 따끈따끈한 논문인 High-Performance Large-Scale Image Recognition Without Normalization에 대한 리뷰입니다. Deepmind에서 새롭게 발표한 일주일도 안된 따끈따끈한 논문입니다. 그동안 ImageNet데이터에서 SOTA 성능을 달성한 논문은 대부분 EfficientNet을 사용하였습니다. 근데 이제 또 새로운 SOTA를 달성한 모델이 나왔습니다. 바로 그 모델이 이 논문에서 소개하는 Nfnet입니다. EfficientNet-B7보다 최대 8.7배 더 빠른 학습 속도로 동등한 성능을 낼 수 있다고 합니다. 뿐만 아니라 가장 큰 NFnet은 86.5 %로 새로운 SOTA를 달성했습니다.
이 논문은 먼저 기존의 모델들에서 너무 당연하게 쓰이고 있었던 배치 정규화에 대한 의문으로부터 시작됩니다.
1. 배치 정규화 (Batch Normalization)
배치 정규화는 좋은 결과를 보여주며 수많은 SOTA 모델에서 많이 사용된 기법입니다. 하지만 저자들은 너무 당연하게 쓰이는 배치 정규화에 대한 의문을 가지고 시작합니다. 사실 배치 정규화는 무조건 좋은 것이 아니라 장단점을 가지고 있습니다.
단점
- 계산 비용이 비싸다.
- 미세 조정(fine-tuning)이 필요한 다른 하이퍼파라미터가 필요해진다.
- 분산 학습에서 많은 구현 에러를 일으킨다.
- 배치 사이즈가 작을 경우 성능이 저하된다.
장점
- 깊은 ResNet에서 residual branch의 스케일을 감소 시킨다. Gradient exploding problem을 줄일 수 있다.
- Mean-shift problem을 해결할 수 있다.
→ 정규화와 훈련 과정을 스무딩한다는 것이 주요 장점
2. NFNets - Normalizer Free Networks란?
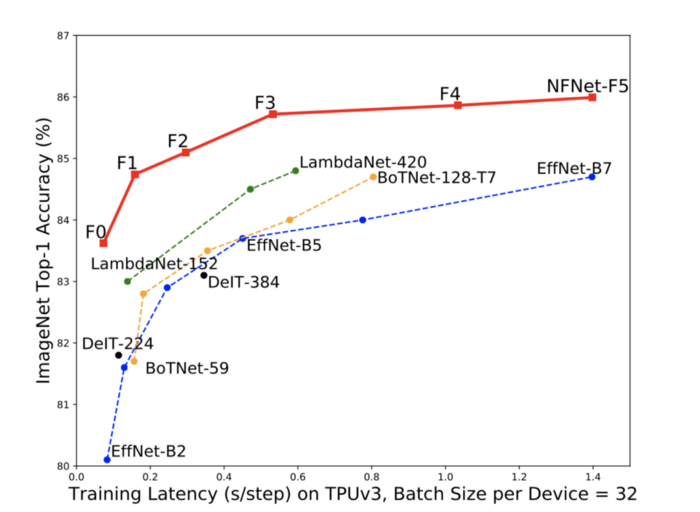
위 그림은 ImageNet에 대한 NFNets에 성능입니다. 보시다시피 기존 SOTA 모델이었던 EfficientNet보다 더 좋은 성능을 보인 것을 알 수 있습니다. 사실 그동안 배치 정규화를 제거하려는 수많은 시도가 있었으나 SOTA 성능에 미치지는 못했습니다. NFNets은 배치 정규화를 제거하고 성공적으로 SOTA를 달성했습니다.
특징
- Adaptive Gradient Clipping(AGC) 제안
- 배치 정규화가 제공했던 정규화 효과를 대체하기 위해 드롭아웃을 사용.
- Sharpness-Aware Minimization(SAM) 사용 (SAM을 좀 수정하여 계산 비용을 20%-40% 절감. 변형된 SAM은 가장 큰 모델 두 종류에서만 사용)
3. Adaptive Gradient Clipping(AGC)
이 논문의 핵심 아이디어 하나는 Adaptive Gradient Clipping(AGC)입니다. 이것을 통해서 배치 정규화가 없이도 모델이 큰 배치에서도 안정적인 성능을 보일 수 있었습니다. AGC는 gradient clipping 기법 중 하나라고 할 수 있습니다. 기존에 모델 학습을 안정화하는 방법으로 gradient clipping이라는 기법이 쓰이곤 했습니다. 이는 기울기가 특정 임계 값을 초과하지 않도록 하여 모델 학습을 안정화하는 것입니다. 이를 이용해 더 큰 learning rate에서도 안정적으로 학습할 수 있어 gradient exploding problem없이 빠른 수렴이 가능했습니다.
논문에서 학습이 안정적으로 이루어지고 있는지를 확인하는 지표로 가중치(weight)의 norm값에 대한 기울기(gradient) norm의 단위 유닛을 이용합니다. 즉, 가중치에 대해 기울기가 얼마나 변했는가를 학습의 안전성을 나타내는 지표로 사용합니다. 이는 $\frac{\Vert{G^l}\Vert}{\Vert{W^l}\Vert}$로 표현할 수 있습니다. 여기서 $l$은 레이어를 $W$는 가중치를, $G$는 기울기를 나타내며, $\Vert{ \cdot }\Vert$은 Frobenius norm을 의미하며 논문에서는 $\Vert{ \cdot }\Vert_F$라 표현되지만 이 글에선 편의를 위해 $_F$를 생략합니다.
이 지표는 한 단계의 경사 하강 알고리즘이 원래의 가중치를 얼마나 변경시키는지에 대한 간단한 지표를 제공합니다. 기울기가 커지면 학습이 불안정하게 되고, 이 경우에 $\frac{\Vert{G^l}\Vert}{\Vert{W^l}\Vert}$가 큰 값을 가지게 됩니다. 따라서 이 값은 기울기를 clip해줘야 할지 말지에 대한 지표가 될 수 있습니다. 실험을 통해 저자는 위 식을 유닛 단위로 구하는 것이 레이어 단위로 구하는 것보다 낫다는 것을 발견했습니다.
위에서 설명한 학습의 안정성을 나타내는 지표를 이용하여 아래의 식으로 clipping합니다. \(G^l_i\rightarrow \begin{cases} \lambda\frac{\Vert{W^l_i}\Vert^\star}{\Vert{G^l_i}\Vert}G^l_i&\text{if } \frac{\Vert{G^l_i}\Vert}{\Vert{W^l_i}\Vert^\star}>\lambda, \\G^l_i &\text{otherwise.} \end{cases} \\\) $\lambda$는 하이퍼파라미터로 clipping을 하는 경계값(threshold)입니다. ${\Vert{W^l_i}\Vert^\star}$은 $\max({\Vert{W^l_i}\Vert^\star},\epsilon)$을 의미합니다. $\epsilon$은 0.001의 값으로 이렇게 처리 해주는 이유는 0으로 초기화 된 파라미터의 기울기가 항상 0으로 클리핑 되는 것을 막기 위해서입니다.
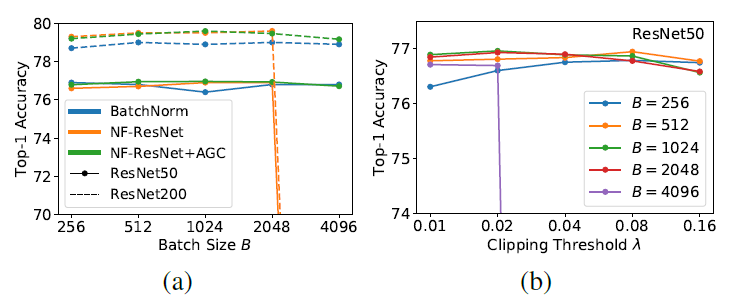
주황색 선과 초록색 선을 비교해보면, AGC를 적용한 결과 배치 정규화가 없이도 큰 batch size에 대해서 성공적으로 학습이 되는 것을 알 수 있습니다.
논문에서 실험으로 밝혀낸 AGC에 대한 사실은 아래와 같습니다.
- 최적의 $\lambda$는 optimizer와 learning rate와 배치 사이즈에 따라 달라지며, 배치 사이즈가 클 수록 작은 $\lambda$를 사용해야 한다.
- 배치 사이즈가 작을 땐 AGC의 효과가 작아진다.
- 마지막 linear layer에는 clipping을 하지 않는게 좋다.
- 첫 번째 convolution을 clipping하지 않고서도 안정적으로 학습할 수 있는 경우가 많다.
AGC 코드 (Pytorch)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#출처: https://github.com/vballoli/nfnets-pytorch
class AGC(optim.Optimizer):
"""Generic implementation of the Adaptive Gradient Clipping
Args:
params (iterable): iterable of parameters to optimize or dicts defining
parameter groups
optim (torch.optim.Optimizer): Optimizer with base class optim.Optimizer
clipping (float, optional): clipping value (default: 1e-3)
eps (float, optional): eps (default: 1e-3)
"""
def __init__(self, params, optim: optim.Optimizer, clipping: float=1e-2, eps: float=1e-3):
if clipping < 0.0:
raise ValueError("Invalid clipping value: {}".format(clipping))
if eps < 0.0:
raise ValueError("Invalid eps value: {}".format(eps))
self.optim = optim
defaults = dict(clipping=clipping, eps=eps)
defaults = {**defaults, **optim.defaults}
super(AGC, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
"""Performs a single optimization step.
Arguments:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
"""
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
param_norm = torch.max(unitwise_norm(
p.detach()), torch.tensor(group['eps']).to(p.device))
grad_norm = unitwise_norm(p.grad.detach())
max_norm = param_norm * group['clipping']
trigger = grad_norm < max_norm
clipped_grad = p.grad * \
(max_norm / torch.max(grad_norm,
torch.tensor(1e-6).to(grad_norm.device)))
p.grad.data.copy_(torch.where(trigger, clipped_grad, p.grad))
return self.optim.step(closure)
AGC 개념은 optimizer를 수정하여 구현할 수 있습니다.. step() 에서 모델의 각 파라미터 정보를 받습니다. param_norm이 논문에서 ${\Vert{W}\Vert^\star}$를, grad_norm이 논문에서 $\Vert{G}\Vert$을 의미합니다. max_norm은 식(1)의 $\frac{\Vert{G^l_i}\Vert}{\Vert{W^l_i}\Vert^\star}>\lambda$ 에서 ${\Vert{W}\Vert^\star}$를 양변에 곱해줘서 구한 오른쪽 항 ${\Vert{W}\Vert^\star}\lambda$ 를 의미합니다.. 최종적으로 gradient 중에 trigger 조건을 만족하는 값은 clipped_grad로 바뀌게 됩니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#출처: https://github.com/vballoli/nfnets-pytorch
def unitwise_norm(x: torch.Tensor):
if x.ndim <= 1:
dim = 0
keepdim = False
elif x.ndim in [2, 3]:
dim = 0
keepdim = True
elif x.ndim == 4:
dim = [1, 2, 3]
keepdim = True
else:
raise ValueError('Wrong input dimensions')
return torch.sum(x**2, dim=dim, keepdim=keepdim) ** 0.5
unitwise_norm 함수는 입력에 대한 Frobenius norm을 unit 단위로 구하는 함수입니다. 만약 모델의 첫번째 컨벌루션 레이어가 입력 채널이 3, 출력 채널이 64, 7x7 커널 사이즈를 갖는다면 optimizer로 들어오는 파라미터는 (64,3,7,7)의 dimension을 갖습니다. 이 파라미터는 unitwise_norm에서 (64,1,1,1)의 dimension의 값으로 return된다.
4. 관련 코드
Tensorflow
Deepmind github에서 official code를 확인할 수 있음.
Pytorch
- Pytorch timm에서 이용 가능. 다만 현재 기준 (2021-02-17) 정식 릴리즈 버전에서는 지원하지 않고 있으므로 해당 프로젝트를 clone하여 이용 가능.
- https://github.com/vballoli/nfnets-pytorch에서 아직 모델은 구현 중이나 논문에서 사용하는 개념(AGC 등)을 적용할 수 있는 모듈 제공